Линейные уравнения задание 9 номер 338495 - Nomertelefona24.ru - большой телефонный справочник предприятий

Образцы заданий № 4 ОГЭ (ГИА-9) Модуль «алгебра»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Образцы заданий № 4

Автор учитель математики

Чагина Юлия Анатольевна

1. 4 № 85. Найдите корни уравнения .

Если корней несколько, запишите их через точку с запятой в порядке возрастания.

2. 4 № 311469. Решите уравнение .

3. 4 № 338480. Решите уравнение

4. 4 № 338488. Решите уравнение

5. 4 № 338495. Решите уравнение

6. 4 № 338500. При каком значении значения выражений и равны?

7. 4 № 338509. Решите уравнение

8. 4 № 338527. Решите уравнение

9. 4 № 338557. Решите уравнение

10. 4 № 338560. Решите уравнение

11. 4 № 338606. Решите уравнение

12. 4 № 338610. Решите уравнение

13. 4 № 338658. Решите уравнение

14. 4 № 338868. Решите уравнение

Если корней несколько, запишите их в ответ в порядке возрастания, через точку с запятой.

1. 4 № 137381. Решите уравнение .

Если корней несколько, запишите их через точку с запятой в порядке возрастания.

2. 4 № 137382. Решите уравнение .

Если корней несколько, запишите их через точку с запятой в порядке возрастания.

3. 4 № 137383. Решите уравнение .

Если корней несколько, запишите их через точку с запятой в порядке возрастания.

4. 4 № 311405. Найдите корни уравнения .

Если корней несколько, запишите их через точку с запятой в порядке возрастания.

5. 4 № 311446. Найдите корни уравнения .

Если корней несколько, запишите их через точку с запятой в порядке возрастания.

6. 4 № 311951. Решите уравнение ( x + 2) 2 = ( x − 4) 2 .

7. 4 № 314495. Найдите корни уравнения

Если корней несколько, запишите их через точку с запятой в порядке возрастания.

8. 4 № 314538. Найдите корни уравнения

Если корней несколько, запишите их через точку с запятой в порядке возрастания.

9. 4 № 320540. Две прямые пересекаются в точке C (см. рис.). Найдите абсциссу точки C .

10. 4 № 320541. На рисунке изображены графики функций и Вычислите координаты точки B .

Запишите координаты в ответе через точку с запятой.

11. 4 № 338180. Уравнение имеет корни −6; 4. Найдите

12. B 4 № 338202. Квадратный трёхчлен разложен на множители: Найдите

13. 4 № 338494. Решите уравнение

14. 4 № 338518. Решите уравнение

15. 4 № 338526. Решите уравнение

16. 4 № 338915. Решите уравнение

Если корней несколько, запишите их через точку с запятой в порядке возрастания.

1. 4 № 311381. Решите уравнение: .

Если корней несколько, запишите их через точку с запятой в порядке возрастания.

2. 4 № 311393. Решите уравнение .

Если корней несколько, запишите их через точку с запятой в порядке возрастания.

3. 4 № 311755. Решите уравнение

4. 4 № 316225. Решите уравнение:

5. 4 № 316341. Решите уравнение:

6. 4 № 338483. Решите уравнение

7. 4 № 338503. Решите уравнение

Если корней несколько, запишите их через точку с запятой в порядке возрастания.

8. B 4 № 338583. Решите уравнение

9. 4 № 338723. Решите уравнение

10. 4 № 338805. Решите уравнение

11. 4 № 338937. Решите уравнение

1. 4 № 311315. Решите систему уравнений

В ответе запишите сумму решений системы.

2. 4 № 311327. Решите систему уравнений

В ответе запишите сумму решений системы.

3. 4 № 311338. Решите систему уравнений

В ответе запишите сумму решений системы.

4. 4 № 311350. Решите систему уравнений

В ответе запишите сумму решений системы.

5. 4 № 311360. Решите систему уравнений

В ответе запишите сумму решений системы.

6. 4 № 311370. Решите систему уравнений

В ответе запишите сумму решений системы.

1. 4 № 314489. Найдите наибольшее значение x , удовлетворяющее системе неравенств

2. 4 № 314490. Найдите наибольшее значение , удовлетворяющее системе неравенств

3. 4 № 314543. Найдите наибольшее значение , удовлетворяющее системе неравенств

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Калькулятор онлайн.
Решение показательных уравнений.

Этот математический калькулятор онлайн поможет вам решить показательное уравнение. Программа для решения показательного уравнения не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения результата.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> С 9 января 2019 года вводится новый порядок получения подробного решения некоторых задач. Ознакомтесь с новыми правилами >> —> Введите показательное уравнение
Решить уравнение

Немного теории.

Показательная функция, её свойства и график

Напомним основные свойства степени. Пусть а > 0, b > 0, n, m — любые действительные числа. Тогда
1) a n a m = a n+m

4) (ab) n = a n b n

7) a n > 1, если a > 1, n > 0

a n m , если a > 1, n n > a m , если 0 x , где a — заданное положительное число, x — переменная. Такие функции называют показательными. Это название объясняется тем, что аргументом показательной функции является показатель степени, а основанием степени — заданное число.

Определение. Показательной функцией называется функция вида y = a x , где а — заданное число, a > 0, ( a neq 1)

Показательная функция обладает следующими свойствами

1) Область определения показательной функции — множество всех действительных чисел.
Это свойство следует из того, что степень a x где a > 0, определена для всех действительных чисел x.

2) Множество значений показательной функции — множество всех положительных чисел.
Чтобы убедиться в этом, нужно показать, что уравнение a x = b, где а > 0, ( a neq 1), не имеет корней, если ( b leqslant 0), и имеет корень при любом b > 0.

3) Показательная функция у = a x является возрастающей на множестве всех действительных чисел, если a > 1, и убывающей, если 0 x при a > 0 и при 0 x при a > 0 проходит через точку (0; 1) и расположен выше оси Oх.
Если х x при a > 0.
Если х > 0 и |х| увеличивается, то график быстро поднимается вверх.

График функции у = a x при 0 0 и увеличивается, то график быстро приближается к оси Ох (не пересекая её). Таким образом, ось Ох является горизонтальной асимптотой графика.
Если х

Показательные уравнения

Рассмотрим несколько примеров показательных уравнений, т.е. уравнений, в которых неизвестное содержится в показателе степени. Решение показательных уравнений часто сводится к решению уравнения a x = a b где а > 0, ( a neq 1), х — неизвестное. Это уравнение решается с помощью свойства степени: степени с одинаковым основанием а > 0, ( a neq 1) равны тогда и только тогда, когда равны их показатели.

Решить уравнение 2 3x • 3 x = 576
Так как 2 3x = (2 3 ) x = 8 x , 576 = 24 2 , то уравнение можно записать в виде 8 x • 3 x = 24 2 , или в виде 24 x = 24 2 , откуда х = 2.
Ответ х = 2

Решить уравнение 3 х + 1 — 2 • 3 x — 2 = 25
Вынося в левой части за скобки общий множитель 3 х — 2 , получаем 3 х — 2 (3 3 — 2) = 25, 3 х — 2 • 25 = 25,
откуда 3 х — 2 = 1, x — 2 = 0, x = 2
Ответ х = 2

Решить уравнение 3 х = 7 х
Так как ( 7^x neq 0 ) , то уравнение можно записать в виде ( frac<3^x> <7^x>= 1 ), откуда ( left( frac<3> <7>right) ^x = 1 ), х = 0
Ответ х = 0

Решить уравнение 9 х — 4 • 3 х — 45 = 0
Заменой 3 х = t данное уравнение сводится к квадратному уравнению t 2 — 4t — 45 = 0. Решая это уравнение, находим его корни: t₁ = 9, t₂ = -5, откуда 3 х = 9, 3 х = -5.
Уравнение 3 х = 9 имеет корень х = 2, а уравнение 3 х = -5 не имеет корней, так как показательная функция не может принимать отрицательные значения.
Ответ х = 2

Решить уравнение 3 • 2 х + 1 + 2 • 5 x — 2 = 5 х + 2 х — 2
Запишем уравнение в виде
3 • 2 х + 1 — 2 x — 2 = 5 х — 2 • 5 х — 2 , откуда
2 х — 2 (3 • 2 3 — 1) = 5 х — 2 ( 5 2 — 2 )
2 х — 2 • 23 = 5 х — 2 • 23
( left( frac<2> <5>right) ^ = 1 )
x — 2 = 0
Ответ х = 2

Решить уравнение 3 |х — 1| = 3 |х + 3|
Так как 3 > 0, ( 3 neq 1), то исходное уравнение равносильно уравнению |x-1| = |x+3|
Возводя это уравнение в квадрат, получаем его следствие (х — 1) 2 = (х + 3) 2 , откуда
х 2 — 2х + 1 = х 2 + 6х + 9, 8x = -8, х = -1
Проверка показывает, что х = -1 — корень исходного уравнения.
Ответ х = -1

ГДЗ задачник по математике 6 класс Бунимович. Решение уравнений и задач с помощью уравнений. Номер №491

Решите уравнение, объясняя каждый шаг решения:
а) 3 x = 2 ;
б) 0,1 x = 5 ;
в)

Решение а

3 x = 2
Чтобы найти неизвестный множитель, нужно частное разделить на известный множитель.

Решение б

0,1 x = 5
Чтобы найти неизвестный множитель, нужно частное разделить на известный множитель.
x = 5 : 0,1
x = 50

Решение в

Решение г

10 : x = 100
Чтобы найти неизвестный делитель, нужно делимое разделить на частное.
x = 10 : 100
x = 0,1

Решение д

x : 5 = 5
Чтобы найти неизвестное делимое, нужно частное умножить на делитель.
x = 5 * 5
x = 25

источники:

http://www.math-solution.ru/math-task/exponential-equality

http://reshalka.com/uchebniki/6-klass/matematika/bunimovich1/589

Источник

Для решения данного номера ученику потребуется знание и умение работать с:

1. Линейными уравнениями. Напомним, что целью преобразований линейного уравнения является получение выражения «неизвестная = число».

2. Квадратными уравнениями. Напомним, что квадратным называется уравнение вида ах2+bx+c=0, корни уравнения находим по формуле

x1,2 =(-b+-(D)1//2) / 2a, где a, b, c –коэффициенты, D=b2-4ac – дискриминант.

Корни квадратного уравнения можно вычислить и по теореме Виета. Кому что нравится, на вкус и на цвет – товарища нет!Рассмотрим характерные примеры.

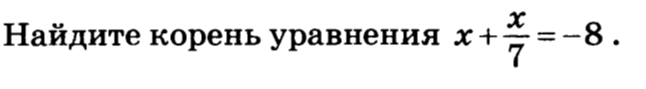
Решение:

1. Данное уравнение линейное, имеет один корень. Найдем его.

2. Избавимся от 7 в знаменателе. Для этого левую и правую части уравнения умножим на 7. Имеем, 7х+х=-8*7 или 8х=-56

3. х=-7

Ответ: -7.

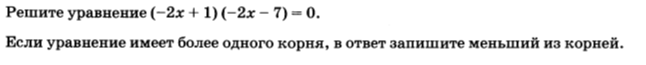
Решение:

1. Преобразуем данное уравнение к стандартной записи квадратного уравнения, для этого перемножим два многочлена. Имеем

4x²+14x-2x-7=0 или 4x²+12x-7=0

2. Дальше решаем по известным формулам

D=12²-4*4*(-7)=144+112=256 дискриминант больше нуля, имеем 2 корня.

3. x₁=(-12+16)/2*4=4/8=1/2=0,5 x₂₌=(-12-16)/2*4=28/8=3,5

4. Выбираем меньший из корней 0,5.

Ответ: 0,5.

Решение:

1. Данное уравнение не надо преобразовывать, поэтому корни уравнения находим по известным формулам.

2. D=(-15)²-4*4*9=225-144=81

3. x₁ =(-(-15)+9)/2*4=24/8=3 x₂==(-(-15)-9)/2*4=6/8=3/4=0,75

4. Выбираем меньший из корней 0,75.

Ответ: 0,75.

Сегодня 18.04.2022 05:02 свежие новости час назад
Прогноз на сегодня : Решу огэ задание 9 . Развитие событий.

Актуально сегодня (18.04.2022 05:02): Решу огэ задание 9

1. Решу огэ задание 9

2. Решу огэ задание 9.3

3. Решу огэ задание 9 русский язык

4. Решу огэ задание 9 информатика

5. Решу огэ задание 9 решите уравнение

6. Решу огэ задание 9 номер 85

7. Решу огэ задание 9 номер 311755

8. Решу огэ задание 9 311755

9. Решу огэ задание 9 311315

10. Решу огэ задание 9 математика

11. Решу огэ задание 93

12. Решу огэ задание 9 85

13. Решу огэ задание 9 316341

14. Решу огэ задание 9 111

15. Решу огэ задание 9 137381

16. Решу огэ задание 9 номер 338606

17. Решу огэ задание 99

18. Решу огэ задание 9.3 русский

19. Решу огэ задание 9 137383

20. Решу огэ задание 9 математика решите уравнение

21. Решу огэ задание 9 номер 316225

22. Решу огэ задание 9 квадратные уравнения

23. Решу огэ задание 9 линейные уравнения

24. Решу огэ задание 9 математика ответы

25. Решу огэ задание 9 алгебра

26. Решу огэ задание 9 311338

27. Решу огэ задание 9 номер 311315

28. Решу огэ задание 9 номер 338495

29. Решу огэ задание 9 137382

30. Решу огэ задание 9 338518

31. Решу огэ задание 9 338509

32. Решу огэ задание 9 номер 338583

33. Решу огэ задание 9 338557

34. Решу огэ задание 9 география

35. Решу огэ задание 9 номер 137381

36. Решу огэ задание 9 номер 338509

37. Решу огэ задание 9 338583

38. Решу огэ задание 9 рациональные уравнения

39. Решу огэ задание 9 338723

40. Решу огэ задание 9 номер 316341

41. Решу огэ задание 9 311381

42. Решу огэ задание 9 номер 311381

43. Решу огэ задание 9 номер 338480

44. Решу огэ задание 9 номер 338488

45. Решу огэ задание 9 номер 338526

46. Решу егэ задание 9 русский язык 2022

47. Решу огэ задание 9 номер 111

48. Решу огэ задание 9.2 русский

49. Решу огэ задание 9 11024

50. Решу огэ задание 9 химия

Решу огэ задание 9

Решу огэ задание 9

Решу огэ задание 9

Решу огэ задание 9
Решу огэ задание 9
Решу огэ задание 9
Решу огэ задание 9
Решу огэ задание 9

Решу огэ задание 9

9041462618282665b80f0416d63c2cfc ef65da3acd36b13df43ff39f4f8b26b4
Решу огэ задание 9
Решу огэ задание 9
Решу огэ задание 9

смотреть сериал игра престолов 2сезон | ирина лисовская зверь читать онлайн не бесплатно полностью | игра пристолов смотреть все серии | дневники вампира 3 сезон 7 серия lostfilm | русский язык 6 класс ладыженская учебник 2 часть ответы гдз | дэк 251 руководство по эксплуатации | сериал друзья 7 сезон смотреть онлайн | скачать базис мебельщик рабочий | гдз татар теле 5 класс шамсутдинова хадиева ответы | инструкция мета акпэ-01 алкотестер руководство |

Invision Community © 2022 IPS, Inc.
Карта сайт Rss
s
p

Источник

Автор:

Мордкович А.Г., Мишустина Т.Н., Тульчинская Е.Е.

ГДЗ(готовые домашние задания), решебник онлайн по алгебре за 9 класс авторов Мордкович, Мишустина(задачи на составление уравнений или систем уравнений) задание(номер) 9 — вариант решения упражнения 9

Глава 1. Неравенства и системы неравенств:

Глава 2. Системы уравнений:

Глава 3. Числовые функции:

Глава 4. Прогрессии:

Глава 5. Элементы комбинаторики, статистики и теории вероятностей:

Глава 1. Домашняя контрольная работа:

Глава 2. Домашняя контрольная работа:

Глава 3. Домашняя контрольная работа:

Глава 4. Домашняя контрольная работа:

Глава 5. Домашняя контрольная работа:

Итоговое повторение:

В данном материале собраны различные задания по данной теме.

Автор: Максименко Евгения Владимировна

Каталог заданий.
Линейные уравнения

Версия для печати и копирования в MS Word

Задание 9 № 85

Решите уравнение 2 минус 3(2x плюс 2)=5 минус 4x .

Ответ:

Решите уравнение дробь: числитель: 5x плюс 4, знаменатель: 2 конец дроби плюс 3= дробь: числитель: 9x, знаменатель: 4 конец дроби .

Ответ:

Решите уравнение: 3 минус дробь: числитель: x, знаменатель: 7 конец дроби = дробь: числитель: x, знаменатель: 3 конец дроби .

Ответ:

Решите уравнение: дробь: числитель: x минус 6, знаменатель: 2 конец дроби минус дробь: числитель: x, знаменатель: 3 конец дроби =3.

Ответ:

Решите уравнение 3x плюс 5 плюс (x плюс 5)=(1 минус x) плюс 4.

Ответ:

Решите уравнение 10x плюс 9=7x.

Ответ:

Решите уравнение минус x минус 2 плюс 3(x минус 3)=3(4 минус x) минус 3.

Ответ:

При каком значении x значения выражений 7x минус 2 и 3x плюс 6 равны?

Ответ:

Решите уравнение 10(x минус 9)=7.

Ответ:

Решите уравнение минус 9(8 минус 9x)=4x плюс 5.

Ответ:

Решите уравнение 1 минус 5x= минус 6x плюс 8.

Ответ:

Решите уравнение 9 минус 2( минус 4x плюс 7)=7.

Ответ:

Решите уравнение 13 плюс дробь: числитель: x, знаменатель: 4 конец дроби =x плюс 1.

Ответ:

Решите уравнение 2x плюс 2= минус 3.

Ответ:

Решите уравнение 4x плюс 7=0.

Ответ:

Решите уравнение дробь: числитель: x, знаменатель: 12 конец дроби плюс дробь: числитель: x, знаменатель: 8 конец дроби плюс x= минус дробь: числитель: 29, знаменатель: 6 конец дроби .

Ответ:

Завершить тестирование, свериться с ответами, увидеть решения.

Каталог заданий.
Линейные уравнения

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Задание 9 № 85

Решите уравнение 2 минус 3(2x плюс 2)=5 минус 4x .

Аналоги к заданию № 85: 338527 338560 311443 311444 311445 311469 311907 314568 338308 338511 … Все

Источник: ГИА по математике 28.05.2013. Основная волна. Вариант 1305.

Раздел кодификатора ФИПИ: 3.1 Решение уравнений и их систем.

Решение

Курс 80 баллов

Сообщить об ошибке · Помощь

Задание 9 № 311755

Аналоги к заданию № 311755: 316315 338485 338501 338578 338581 338692 338719 338871 338882 338901 … Все

Раздел кодификатора ФИПИ: 3.1 Решение уравнений и их систем.

Решение

Курс 80 баллов

Сообщить об ошибке · Помощь

Аналоги к заданию № 316225: 316252 316278 338555 338778 338620 338622 338693 338738 338774 338840 … Все

Источник: Диагностическая работа 01.10.2013 Вариант МА90105

Раздел кодификатора ФИПИ: 3.1 Решение уравнений и их систем.

Решение

Курс 80 баллов

Сообщить об ошибке · Помощь

Задание 9 № 316341

Аналоги к заданию № 316341: 316367 Все

Раздел кодификатора ФИПИ: 3.1 Решение уравнений и их систем.

Решение

Курс 80 баллов

Сообщить об ошибке · Помощь

Задание 9 № 338480

Решите уравнение 3x плюс 5 плюс (x плюс 5)=(1 минус x) плюс 4.

Раздел кодификатора ФИПИ: 3.1 Решение уравнений и их систем.

Решение

Курс 80 баллов

Сообщить об ошибке · Помощь

Пройти тестирование по этим заданиям

Вы должны авторизоваться, чтобы ответить на задание. Пожалуйста, войдите в свой профиль на сайте или зарегистрируйтесь.

Линейные уравнения задание 9 номер 338495

Самарина Светлана Дмитриевна

04.05.2020.
Тест. Алгебра, 9 класс

Внимание! Все тесты в этом разделе разработаны пользователями сайта для собственного
использования.
Администрация сайта не
проверяет возможные ошибки,
которые могут встретиться в тестах.

Тест содержит 8 линейных уравнений, на выполнение теста отводится 10 минут

Вопрос 1

Линейные уравнения задание 9 номер 338495

Вопрос 2

Линейные уравнения задание 9 номер 338495

Вопрос 3

Линейные уравнения задание 9 номер 338495

Вопрос 4

Линейные уравнения задание 9 номер 338495

Вопрос 5

Линейные уравнения задание 9 номер 338495

Вопрос 6

Линейные уравнения задание 9 номер 338495

Вопрос 7

Линейные уравнения задание 9 номер 338495

Вопрос 8

Линейные уравнения задание 9 номер 338495

5 балльная

Оценка
Необходимый минимум баллов, %
Альтернативное название

Зарегистрироваться

Или войти с помощью аккаунта в соцсети

Войти в профиль

Вспомнить пароль

Или войти с помощью аккаунта в соцсети

Джамиля Агишева

При выполнении задания 9 ОГЭ по математике необходимо:

уметь решать линейные и квадратные уравнения, системы уравнений и неравенств.

Пример 1. Решите уравнение $-x-4+5left(x+3right)=5left(-1-xright)-2$ .

Решение. Уравнение линейное. Раскрываем скобки, приводим подобные слагаемые, все «иксы» переносим в левую часть равенства, всё без «иксов» – вправо:

$-x-4+5x+15=-5-5x-2 Rightarrow 4x+11=-5x-7 Rightarrow$

$Rightarrow 4x+5x=-11-7 Rightarrow 4x+5x=-11-7 Rightarrow 9x=-18 Rightarrow x=-2.$

Ответ: — 2.

Пример 2. Решите уравнение $frac{5}{4}x^2+7x+9=0$ . Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.

Решение. Уравнение является квадратным $a=frac{5}{4}$ , $b=7$ , $c=9$ . Вычисляем дискриминант и корни:

$D=b^2-4ac=7^2-4cdot frac{5}{4}cdot 9=49-45=4.$

$x_{1,2}=frac{-bpm sqrt{D}}{2a}=frac{-7pm sqrt{4}}{2 cdot frac{5}{4}}=frac{-7pm 2}{frac{5}{2}}=(-7pm 2)cdot frac{2}{5} Rightarrow left[ begin{array}{c}x_1=left(-7-2right)cdot frac{2}{5}=-9cdot 0,4=-3,6, x_2=left(-7+2right)cdot frac{2}{5}=-5cdot 0,4=-2. end{array}right.$

Ответ: $-3,6-2$ .

Пример 3. Решите уравнение $(-4x-3)(x-3)=0$ . Если уравнение имеет более одного корня, в ответ запишите меньший из корней.

Решение. В левой части данного уравнения произведение двух множителей-скобок, и это произведение равно нулю. Это возможно тогда и только тогда, когда хотя бы один из множителей равен нулю. Значит, получаем два уравнения:

Линейные уравнения задание 9 номер 338495

Тогда меньший из корней уравнения равен -0,75.

Ответ: -0,75.

Пример 4. Решите систему уравнений $left{ begin{array}{c}3x+2y=8, 4x- y =7. end{array}right.$

В ответе запишите значение $x+y$ .

Решение. Используем метод подстановки: из второго уравнения можно выразить y и подставить в первое уравнение.

$left{ begin{array}{c}3x+2(4x-7)=8, y=4x-7. end{array}right. Rightarrow left{ begin{array}{c}3x+8x-14=8, y=4x-7. end{array}right.Rightarrow$

$Rightarrow left{ begin{array}{c}x=2, y=4cdot 2-7=1. end{array}right.$

Таким образом, $x+y=2+1=3$ .

Пример 5. На рисунке изображены графики функций $y=4-x^2$ и $y=-2-x$ . Вычислите ординату точки B.

Линейные уравнения задание 9 номер 338495

Решение. Для нахождения координат точек пересечения графиков заданных функций необходимо решить систему уравнений.

$left{ begin{array}{c}y=4-x^2, y=-2-x. end{array}right. Rightarrow left{ begin{array}{c}-2-x=4-x^2, y=-2-x. end{array}right.Rightarrow$

$Rightarrow left{ begin{array}{c}x^2-x-6=0, y=-2-x. end{array}right.$

Найдём корни первого уравнения системы.

$x^2-x-6=0.$

$D=(-1)^2-4cdot1cdot(-6)=1+24=25.$

$x_{1,2}=frac{1pmsqrt{25}}{2cdot1}=frac{1pm5}{2}Rightarrowleft[ begin{array}{c} x_1=frac{1-5}{2}=-2, x_2=frac{1+5}{2}=3. end{array} right.$ ̶ абсцисса точка B.

Тогда ордината точки В: $y=-2-x=-2-3=-5.$

Ответ: -5.

Пример 6. Найдите наибольшее значение x, удовлетворяющее системе неравенств:

$left{ begin{array}{c}8x+16le 0, 2-2xtextless13. end{array}right.$

Решение. Выразим из каждого неравенства переменную x. Не забываем, что при делении обеих частей неравенства на положительное число знак неравенства не меняется, при делении на отрицательное число ̶ знак неравенства меняется на противоположный.

$left{ begin{array}{c}8x+16le 0, 2-2xtextless13. end{array}right. Rightarrow left{ begin{array}{c}8xle -16, -2xtextless13-2. end{array}right. Rightarrow left{ begin{array}{c}8xle -16, |:8 -2xtextless11. |:(-2) end{array}right. Rightarrow$

$Rightarrowleft{ begin{array}{c}xle -2, xtextgreater-5,5. end{array}right.$

Используем числовую прямую. Решение первого неравенства отметим штриховкой («ёлочкой») с наклоном вправо, второго неравенства ̶ штриховкой с наклоном влево. При этом точка -2 будет «закрашенной», т.к. знак первого неравенства нестрогий, а точка -5,5 будет «выколотой», т.к. знак второго неравенства строгий.

Линейные уравнения задание 9 номер 338495

Решением системы неравенств является тот промежуток, на котором пересеклись две «ёлочки», то есть две штриховки. Это промежуток $(-5,5;-2]$ . «Выколотой» точке соответствует круглая скобка, «закрашенной» ̶ квадратная.

Ответим на вопрос задачи. Наибольшее значение $x=-2.$

Ответ: $-2$ .

ОГЭ №9. Линейные, квадратные и рациональные уравнения. Системы уравненийadmin2019-09-09T22:03:22+03:00

Скачать файл в формате pdf.

Источник

В девятом задании модуля алгебра ОГЭ по математике нам предлагают решить уравнения. Это могут быть как линейные уравнения, которые решаются переносом всех известных членов в одну сторону, а неизвестных (x) в другую, так и квадратные уравнения, которые в свою очередь могут быть полными и неполными.

Судя по материалам ОГЭ и практике проведения экзамена, наиболее вероятным заданием может быть решение линейного или квадратного уравнения. Тем не менее мы рассмотрим задания по всей этой тематике. Сложность заданий как всегда возрастает от задания к заданию.

Ответом в задании №9 является целое число или конечная десятичная дробь.

Теория к заданию №9

Ниже я привел теорию по решениям линейных и квадратных уравнений:

Схема решения, правила и алгоритм действий при решении линейного уравнения:

решение линейного уравнения

Схема решения, правила и порядок действий при решении квадратного уравнения:

решение квадратного уравнения

В трех типовых вариантах я разобрал данные случаи — в первом варианте вы найдете подробные указания по решению линейных уравнений, во втором разобран пример решения неполного квадратного уравнения, а в третьем — решение полного квадратного уравнения с вычислением дискриминанта.

Разбор типовых вариантов задания №9 ОГЭ по математике

Первый вариант задания (линейные уравнения)

Найдите корень уравнения:

10 ( x — 9 ) = 7

Решение:

Данное уравнение представляет собой обыкновенное уравнение первой степени и решается переносом всех известных частей в правую часть, оставив x слева.

Для начала следует раскрыть скобки: 10x — 90 = 7

Затем переносим 90 в правую часть (не забываем поменять знак):

10x = 7 + 90

10x = 97

Затем делим обе части на 10:

x = 9,7

Ответ: 9,7

Второй вариант задания (неполные квадратные уравнения)

Решите уравнение:

3 x² + 12 x = 0

Решение:

Это неполное квадратное уравнение, в котором не обязательно вычислять дискриминант, а достаточно вынести x за скобку:

x ( 3 x + 12 ) = 0

Произведение множителей тогда равно нулю, когда один из множителей равен нолю:

x = 0

или

3 x + 12 = 0

3 x = -12

x = -4

Так как в ответе просят указать наименьший корень, то это -4.

Ответ: -4

Третий вариант задания (квадратные уравнения)

Решите уравнение:

8 x² — 10x + 2 = 0

Решение:

Уравнение является полным квадратным уравнением, поэтому классическим вариантом решения является вычисление дискриминанта. Но в данном случае можно заметить, что все множители кратны двум, поэтому можно все уравнение разделить на 2 для удобства вычисления:

4 x² — 5x + 1 = 0

Далее вычисляем дискриминант:

D = b² — 4ac

D = 5² — 4 •4•1 = 9

Вычисляем корни:

x = (- b — √D) / 2a = (5 — 3 )/ 2 •4 = 0,25

x = (- b + √D) / 2a = (5 + 3 )/ 2 •4 = 1

Так как нам нужно выбрать меньший из корней по условию, то выбираем 0,25

Ответ: 0,25

Четвертый вариант задания (демонстрационный вариант ОГЭ 2017)

Решите уравнение:

7х — 9 = 40

Решение:

В данной задаче нам предстоит решить линейное уравнение. Подход к решению таких уравнений достаточно простой — всё, что известно переносим в правую часть, всё, что неизвестно — оставляем в левой. Далее выполняем необходимое арифметическое действие.

Решение:

7х — 9 = 40

Переносим 9 в правую часть (не забываем про смену знака):

7х = 40 + 9, что эквивалентно

7х = 49

х в нашем случае — это неизвестный множитель, следовательно, чтобы его найти, делим произведение на известный множитель:

х = 49/7, откуда

х = 7

Ответ: 7

Пятый вариант задания (рациональные уравнения)

Найдите корень уравнения:

Решение:

Прежде всего, исключим корень, который не входит в ОДЗ:

x+6≠0 → х≠–6

Далее решаем уравнение.

Представляем число 2 в уравнении справа в виде дроби 2/1. Уравнение получает вид пропорции:

Применим правило пропорции. Перемножим между собой крайние ее члены и средние:

1·1=(х+6)·2

Выполним умножение в левой части уравнения и раскроем скобки справа:

1=2х+12

Поменяем местами левую и правую части уравнения, чтобы оно приняло привычный вид:

2х+12=1

Переносим 12 из левой части в правую:

2х=1–12

2х=–11

Находим корень:

х=–11/2=–5,5

ОДЗ это значение не исключает, поэтому оно является искомым результатом.

Ответ: –5,5

Шестой вариант задания(рациональные уравнения)

Найдите корень уравнения:

Решение:

Обе части уравнения приводим к единому знаменателю 12:

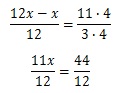
Задание №9 ОГЭ по математике

Т.к. знаменатели в левой и правой частях уравнения одинаковы, не равны нулю и не содержат переменных, то их можно сократить (т.е. ими можно пренебречь). Тогда получаем:

11х=44

х=44:11

х=4

Ответ: 4

Источник

- Предмет:
  
  Алгебра
- Автор:
  
  jamarigraves116
- Создано:
  
  3 года назад
Ответы

Знаешь ответ? Добавь его сюда!

Литература

3 минуты назад

Как Евгений Онегин изменился к концу романа(кто читал)?
Алгебра

3 минуты назад

(10m+8n³)( 10m — 8n³) =пж
Химия

3 минуты назад

какой цвет будет если смешать фенолфталеин с поваренной солью
Геометрия

3 минуты назад

A
3.20. Пусть S-площадь параллелограмма, а —
Доведенная к основанию. Заполните следующую таблицу:
h
S
7
8
2
12
2√2
А
8
6
1
2
2
-T/N
7
основание, һ — вы-
4
√3
7
2/64/7
Даю 100 баллов помогите
Русский язык

3 минуты назад

Подумай что общего у этих слов и чем они различаются Составь и запиши предложение с любым словом.
норка
лисички
овсянка

Информация

Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.

Вы не можете общаться в чате, вы забанены.

Чтобы общаться в чате подтвердите вашу почту
Отправить письмо повторно

Вопросы без ответа

Геометрия

1 час назад

ПОМОГИТЕ СРОЧНО! C) укажите признак параллельности прямых, если прямые а и параллельны, если нет — поставьте прочерк.
Английский язык

6 часов назад

ДЗ английский 8 класс. Помогите, пожалуйста!

Топ пользователей

Fedoseewa27

21183
Sofka

7416
vov4ik329

5112
DobriyChelovek

4620
zlatikaziatik

3750
olpopovich

3461
manbenzopila

2540
Udachnick

1867
Zowe

1683
ViktoriaBell0

1255

Войти через Google

или

Запомнить меня

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

Выберите язык и регион

Русский

Россия

English

United States

zoom

How much to ban the user?

1 hour
1 day

Источник

Решите систему уравнений 0f6f2de8fd09c78d5777712eea46ac7a В ответ запишите х + у.

Разделим обе части первого уравнения на 2 и решим систему методом подстановки:

893314cf6ad585f73cc37cce1951c4c8

Искомая сумма равна 3,5.

Систему можно было бы решить методом алгебраического сложения:

aa5723df2f283a0e8e2378409f06a1fe

Решите систему уравнений 9c153709529757b85af5d5e88a2dda03 В ответ запишите х + у.

Решим систему методом подстановки:

cd25901257ea66178b9e159765a92744

Искомая сумма равна 5.

Решите систему уравнений 92186c09f51cfd26c9ae27e6d72699ed В ответ запишите х + у.

Решим систему методом подстановки:

4e85f7026745c9a5ea3c65f5dc3a3004

Искомая сумма равна 3.

Решите систему уравнений a9ad4149b538629c43d25db4f58ecd99 В ответ запишите х + у.

Решим систему методом подстановки:

3e95bcbe344151b78146062e60fdc280

Искомая сумма равна −1.

Решите систему уравнений 54a1ecbfd196b1ab0a17bde2deb1e825 В ответ запишите х + у.

Решим систему методом подстановки:

a31e3f3da3dc74e2fe4d0595a7149f83

Искомая сумма равна 5.

Решите систему уравнений d87fbb53fbce2ab5f5821fd48a3bb581 В ответ запишите х + у.

Решим систему методом подстановки:

7b5fb5b1c6c720b6ea2dd103dff0f62e

Искомая сумма равна 1.

Решите систему уравнений c35be042cc73f14b78ab152b46ca6349

Выразим переменную 415290769594460e2e485922904f345d из второго уравнения и подставим в первое:

4a13556276ea6596933cfde15bac8905

Решим первое уравнение системы. Пусть 1ae60b4b68fc7cf49d684965a27f56a8

9b3c3feeced8a29594b006c593a653fc

Тогда 09d0318256e152524eb8baf781089ec9

Система имеет четыре пары решений:

2be60bf0ce4c8a19f486f498f3da259a

Ответ: (−1; −6); (1; 6); (−6; −1); (6; 1).

Решите систему уравнений 68e16c07d798c9900fc1127097ef1ae4

Преобразуем систему уравнений:

c2f075d4c48204feb28d175afdc168b8

откуда получаем решения системы уравнений : (2; −1) и (2; 1).

откуда здесь получилось 22=11х? можно расписать подробнее?

Алина, домножили на два верхнюю часть и после этого сложили с нижней.

Решите систему уравнений 5346f77a57f1580a06f65d0417b59ff5

Выразим одну переменную через другую из второго уравнения и подставим полученное выражение в первое уравнение

2f349d9059afebfed4ac6ea0a7309983

d1aa1ee8bfbb7ade30c55e28ee85acd1

Заметим, что пара корней 1a8c9cadcabef2586774f505f7d5f892 не является корнями уравнения, потому что при 06cbb897f7d9cee2a039bd51f65afe9b знаменатель второго уравнения обращается в ноль.

Приведем решение Анны Мечевой.

Заметим, что выражение 31b30e7ca9e4a8121600e1fa1f51504c обращается в 0 при x = 4 или y = 6. Подставим эти значения во второе уравнение.

0b7bcf63bfc0c91f3f974d5dfb6c7853 Это уравнение не имеет решений.

51ad7d5d001e7c0c86196de27aeafccb

Следовательно, решением уравнения является пара чисел (3, 6).

Решите систему уравнений 4b41739e3994eebe7d6058f8547a9d04

Из второго уравнения системы получаем 74cd653737a860e1666d09dc0d7c3474 Первое уравнение системы принимает вид

904c0645c3c873055acd0edb207d21a9

Уравнение x 2 = 1 имеет корни x = −1 и x = 1.

Уравнение x 2 = 9 имеет корни x = −3 и x = 3.

Значит, решение исходной системы: (−1; −3), (1; 3), (−3; −1) и (3; 1).

Ответ: (−1; −3), (1; 3), (−3; −1); (3; 1).

Аналоги к заданию № 338894: 341366 Все

Решите систему уравнений d88e9c4d777ba3dfec639c12a2378bba

Подставим 8e69514c62485799108d77123dbe885d во второе уравнение системы, получим уравнение относительно bbae8b8558eb5aa07dd6b8ddf06a7bb6 . Отсюда 5870bb658ee9e8a6900c138365d64c80 . Подставим в уравнение , получим: ad35dddd61e5fe3b379ee629d289c799

Решите систему уравнений 5a0db349a6091eaa5c1d388a64b5817d

Подставим cef09cba15b906b1aa035801f2edc7be во второе уравнение системы, получим уравнение относительно 35df6ed7e5b57c26d96ec4aadccf6b62 . Отсюда af07dfc8b83b5fc76fe44150be234258 и 52805d388d4a07409473f3998a5e013d . Подставим и в уравнение cef09cba15b906b1aa035801f2edc7be , получим: 02600edee9cf21beb48df14d3e124ac7 и 9830b0ed5a957ff5ebfc7624a5ed45c5 соответственно.

Источник

Задание 9 номер 311315

Решите систему уравнений 54a1ecbfd196b1ab0a17bde2deb1e825 В ответ запишите х + у.

Решим систему методом подстановки:

a31e3f3da3dc74e2fe4d0595a7149f83

Искомая сумма равна 5.

Найдите корни уравнения 32201b9a05dfe1f389efcf6c7d4f7810

Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.

Запишем уравнение в виде:

3f584095cb0e6d5569d49ae038d674b5

По теореме Виета, сумма корней равна 5, а их произведение равно 4. Тем самым, это числа 4 и 1.

Решите уравнение e94552ea0155de88b6d42a2d9060db50 .

Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.

По теореме, обратной теореме Виета, сумма корней равна 1, а их произведение −6.

Тем самым, это числа −2 и 3.

Решите уравнение 5d0b3795f2a7f2d98860dde76b8158da

Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.

Умножим обе части уравнения на 89c090488479a41cad9954347908e91c

d9f048a5ae1c1425c22291decd51ea6d

Решите систему уравнений 9036a91838716ff808f5f8769604a9b6

Выразим переменную y из одного уравнения и подставим во второе:

f9993bcfe2744687461af09b34467733

a932b87df0df2e9efee6422adb10d330

Андрей, спасибо, правка внесена.

Решите уравнение: f647b29cbb6e05e4e7d73b98866565fe .

Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.

Используем свойство пропорции.

bc6de5d066e6dee122e94be0fe3b673d

Найдите корни уравнения ed2f470d6c38f0c9d7632608747811e4 .

Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.

616fe4530bfc2e13b784c24be3496b01

Решите уравнение: 2b17be08fcc6ed889298cc30dd9a8fe5

Раскладывая на множители левую часть уравнения, получаем 469e6ad9b9a5dc0118333747ca86ddaa Таким образом, корни уравнения 7492a0f5fab843253d92bb5cc7ad623c

Ответ: df7ce3c031669df7a4296d77d8820bb9

а почему исчезло 24? никаких предпосылок для этого я не вижу

Гость, раскройте скобки.

Решите систему f7fcbfc2a6ed04cb3ccf9debb8e9b673

Вычтем из первого уравнения второе, используем формулу разности квадратов, затем метод подстановки:

5147878b278c3cbfd53a2cd59ab0914b

fa7d4de22554eb68319fc62c81e62194

Ответ: 2fde3ff0601cfa64bc0b512ea854bb68

Решите систему уравнений 617821655edeca2a956bc99198bc6098

4b720b4b8cf491bebf32863b20d4b7df

f1221ffb03e74b055bb1fba375c58b32

Ответ: b80f3032cf644b8fdca3b818f2fb9a98

Решите уравнение acbc3ad34bfc8ae89a8d991030aefdaa

Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.

33231ecbd3112b7984aa6f34a900c14e

Один из корней уравнения 11a713562c9c7cac4eeaf66f02898629 равен −1. Найдите второй корень.

Подставим известный корень в уравнение: 62ca9539977a71ded532df68f2a65bcd . Получим уравнение относительно 6f8f57715090da2632453988d9a1501b . Решим его: a5bb8d9fafc29b4e7e4374ba283bece3 . Подставим в уравнение: b924fa475e2b91cd9a55ca5f52f217b9 , откуда

c917a325eaf1396e20f06f8afad40583

Ответ: 27a1bc1409fd221aee39ac7a9b713418

Источник

Задание 9 номер 311315

Решите систему уравнений 0f6f2de8fd09c78d5777712eea46ac7a В ответ запишите х + у.

Разделим обе части первого уравнения на 2 и решим систему методом подстановки:

893314cf6ad585f73cc37cce1951c4c8

Искомая сумма равна 3,5.

Систему можно было бы решить методом алгебраического сложения:

aa5723df2f283a0e8e2378409f06a1fe

Решите систему уравнений 9c153709529757b85af5d5e88a2dda03 В ответ запишите х + у.

Решим систему методом подстановки:

cd25901257ea66178b9e159765a92744

Искомая сумма равна 5.

Решите систему уравнений 92186c09f51cfd26c9ae27e6d72699ed В ответ запишите х + у.

Решим систему методом подстановки:

4e85f7026745c9a5ea3c65f5dc3a3004

Искомая сумма равна 3.

Решите систему уравнений a9ad4149b538629c43d25db4f58ecd99 В ответ запишите х + у.

Решим систему методом подстановки:

3e95bcbe344151b78146062e60fdc280

Искомая сумма равна −1.

Решите систему уравнений 54a1ecbfd196b1ab0a17bde2deb1e825 В ответ запишите х + у.

Решим систему методом подстановки:

a31e3f3da3dc74e2fe4d0595a7149f83

Искомая сумма равна 5.

Решите систему уравнений d87fbb53fbce2ab5f5821fd48a3bb581 В ответ запишите х + у.

Решим систему методом подстановки:

7b5fb5b1c6c720b6ea2dd103dff0f62e

Искомая сумма равна 1.

Решите систему неравенств

eb4410f9a9e20cd2ad0869f30cc64787

На каком рисунке изображено множество её решений?

В ответе укажите номер правильного варианта.

311cd42a62ef69b83793a2c15d704153

Решением системы является отрезок, изображённый под номером 2.

Правильный ответ указан под номером 2.

Решите систему неравенств 9f2ae2d8b65c55e25e99ed80bfdd2b38

На каком из рисунков изображено множество её решений?

В ответе укажите номер правильного варианта.

fd7954974fec6c4525396c22aed074ce

Правильный ответ указан под номером 3.

Решите систему неравенств ec45eefa3cc457818fc503e9c36f359b

На каком рисунке изображено множество её решений?

В ответе укажите номер правильного варианта.

Решим систему неравенств:

17692ef9ef88fe70b77d777ebf90d0c6

Решение неравенства изображено под номером 4.

Решите систему неравенств dfceb7b83b4570b929b5fceb6d53d61e

Решим первое неравенство системы:

7e6ad3243d8c98ba5fb8923b731781d8

Выражение 940f261f322bb288973afa6a813e9722 всегда больше нуля поэтому данное неравенство эквивалентно неравенству fe8ba0139de1c97ad9da6daaf9d9ecff

Решим второе неравенство:

1862cd40a7ca3af94edca86254ba16f9

Пересекая решения обоих неравенств, получим, что решением системы является отрезок 3c8f6994bf53dbd238c78686675b4d7d

Ответ: 3c8f6994bf53dbd238c78686675b4d7d

Можно сразу заметить, что в знаменателе первого выражения стоит квадрат числа плюс положительное число, значит, знаменатель всегда больше нуля.

Решите систему уравнений c35be042cc73f14b78ab152b46ca6349

Выразим переменную 415290769594460e2e485922904f345d из второго уравнения и подставим в первое:

4a13556276ea6596933cfde15bac8905

Решим первое уравнение системы. Пусть 1ae60b4b68fc7cf49d684965a27f56a8

9b3c3feeced8a29594b006c593a653fc

Тогда 09d0318256e152524eb8baf781089ec9

Система имеет четыре пары решений:

2be60bf0ce4c8a19f486f498f3da259a

Ответ: (−1; −6); (1; 6); (−6; −1); (6; 1).

Решите систему уравнений 68e16c07d798c9900fc1127097ef1ae4

Преобразуем систему уравнений:

c2f075d4c48204feb28d175afdc168b8

откуда получаем решения системы уравнений : (2; −1) и (2; 1).

откуда здесь получилось 22=11х? можно расписать подробнее?

Алина, домножили на два верхнюю часть и после этого сложили с нижней.

Решите систему неравенств f66541e91df7ed0402a5affe35ac7a7d

Используя тот факт, что знаменатель первого неравенства всегда больше нуля, преобразуем систему неравенств:

800fef7d8ab64639d8c4de7cb39616ec

А куда делся знаменатель в первой части? Его можно просто так выкидывать?

Никита, знаменатель в первом уравнении всегда больше ноля, поэтому мы его не учитываем.

Решите систему неравенств 05493fd60f482e660cc968339d9419f5

Преобразуем систему неравенств:

6e54066150b5c2fa2d7ddbcd5392f007

Аналоги к заданию № 338522: 341418 Все

Решите систему уравнений d88e9c4d777ba3dfec639c12a2378bba

Решите систему уравнений 5a0db349a6091eaa5c1d388a64b5817d

Источник

Образцы заданий № 4 ОГЭ (ГИА-9) Модуль «алгебра»

Решение задач по математике онлайн

Калькулятор онлайн.Решение показательных уравнений.

Немного теории.

Показательная функция, её свойства и график

Показательные уравнения

ГДЗ задачник по математике 6 класс Бунимович. Решение уравнений и задач с помощью уравнений. Номер №491

Решение а

Решение б

Решение в

Решение г

Решение д

Решу огэ задание 9

Решу огэ задание 9

Решу огэ задание 9

Решу огэ задание 9

Глава 1. Неравенства и системы неравенств:

Глава 2. Системы уравнений:

Глава 3. Числовые функции:

Глава 4. Прогрессии:

Глава 5. Элементы комбинаторики, статистики и теории вероятностей:

Итоговое повторение:

Вопрос 1

Вопрос 2

Вопрос 3

Вопрос 4

Вопрос 5

Вопрос 6

Вопрос 7

Вопрос 8

5 балльная

Зарегистрироваться

Войти в профиль

Теория к заданию №9

Разбор типовых вариантов задания №9 ОГЭ по математике

Первый вариант задания (линейные уравнения)

Решение:

Второй вариант задания (неполные квадратные уравнения)

Решение:

Третий вариант задания (квадратные уравнения)

Решение:

Четвертый вариант задания (демонстрационный вариант ОГЭ 2017)

Решение:

Пятый вариант задания (рациональные уравнения)

Решение:

Шестой вариант задания(рациональные уравнения)

Решение:

Задание 9 номер 311315

Задание 9 номер 311315

Не пропустите также:

Калькулятор онлайн.
Решение показательных уравнений.